| PREVIOUS PRESENTATION | BACK TO PROGRAM OVERVIEW | NEXT PRESENTATION |
Time-domain Experiments on Fluctuating Quantities: Photons and Spins
Alfred Leitenstorfer1
1Department of Physics and Center for Applied Photonics, University of Konstanz, D-78457 Konstanz, Germany
Time-domain terahertz spectroscopy and experiments tracing ultrafast phenomena in general are typically based on the pump-probe principle: an ultrashort laser pulse termed “pump” initiates a process via some coupling mechanism between light and matter. A second pulse termed “probe” is derived from the same pulse train and reads out changes of a physical property as a function of time with respect to the arrival of the pump, as set by an optical delay stage. Typically, the difference between pump on and off is detected e.g. by a lock-in scheme to optimize the signa-to-noise ratio. In this way, the average change of the probed parameter is obtained for each time delay. Since some years, experiments are emerging which go beyond this stage by not only detecting average quantities but also their fluctuations. Initially, we realized that ultrabroadband electro-optic sampling had become sensitive enough to eventually detect the vacuum noise of the mid-infrared radiation field. The principle of these experiments was as follows: First, the signals from an electro-optic detector system were taken without a coherent input and these readouts were stored in a histogram. In a second stage, the probe pulse was stretched in time such that the detection bandwidth collapsed, leaving no more sensitivity to the vacuum noise but keeping the trivial fluctuations due to the shot-noise of probe photons identical. It turned out that the histogram in this second state became narrower by a few percent as compared to the first one which contained also the vacuum signals [1]. Alternatively, the transverse cross section of the space-time volume probed was varied by translating the electro-optic crystal through the confocal region of the probe beam. As in the first case, the result was close to the one predicted by the first quantum theory of electro-optic sampling which was based on a first-order perturbative approach to field quantization of the nonlinear process with paraxial mode functions [2]. In this study, great care had to be taken such that the mechanical translation of optical components to stretch the probe volume longitudinally or in the transvers direction did not influence the flux of probe photons e.g. due to imperfections of optical surfaces. Consequently, it became highly desirable to modulate the quantum vacuum by some nonlinear process and detect the resulting deviations from the level of vacuum noise all-optically. To this end, we were aiming to produce mid-infrared squeezed states as a signal for electro-optic detector. By comparing the noise level of this input with the one due to bare vacuum noise as a function of time delay, a temporal pattern should emerge with alternating regions of excess noise and reduced fluctuations. We readily found such signatures [3] which seemed consistent with theoretical predictions [2].
In parallel, Jerôme Faist’s team at ETH Zurich implemented a scheme where two readout pulses for electro-optic sampling are time delayed with respect to each other and adjusted such that they probe transversely separated spatial regions in a detector crystal which are close enough to belong to the same terahertz transverse mode. This feature is enabled by the large difference in wavelength between the 800 nm probe beam and the detected frequency interval around 1 THz. Initially sensing thermal fluctuations, they succeeded to detect correlations due to vacuum fluctuations when cooling down the entire setup to a temperature of 4 K [4]. Amazingly, the experiment demonstrated that it is possible to e.g. characterize the spectral response of an electro-optic setup solely with this vacuum input. When trying to extend our squeezing measurements [2] by exploiting a more powerful pump source for modulating the quantum vacuum [5], we were able to reproduce the initial results. Unfortunately, we also obtained signatures at higher intensities that were no longer compatible with the original interpretation [2] of a cascaded process where first a coherent field transient is generated by optical rectification and subsequently squeezes the quantum vacuum in the same second-order nonlinear crystal. It turned out that the coherent amplitude detected in parallel in these experiments was the source for severe artefacts: When a slight deviation from a quarter-wave phase shift in the ellipsometer of the electro-optic setup occurs due to e.g. focusing onto the detector diodes with curved metallic mirrors [6], some implicit signal emerges due to the Hilbert transform of the coherent input transient which is of opposite sign in the upper and lower spectral parts of the probe [6]. Due to this sign flip, this signal does not leave a trace in the coherent amplitude but it alters the noise readout because of the presence of some anti-correlated amplitude fluctuations in the extreme spectral regions of the probe [7]. In this way, the noise deviations detected in Ref. 2 exceeded the ones we now estimate due to real squeezing effects by about two orders of magnitude.
The measures required to eventually reach a reliable technology based on generation and detection of nonclassical states of mid-infrared light in the time domain is as follows: Most importantly, e.g. a squeezed vacuum with large temporal deviations from zero-point fluctuations has to be generated and any co-propagating coherent field amplitudes have to be suppressed as much as possible. We intend to meet these requirements by pumping a spontaneous parametric downconverter that squeezes the vacuum in a polarization direction perpendicular to the coherent and intense excitation beam which is derived from a degenerate optical parametric oscillator pumped synchronously with a phase-stable input [8]. In parallel, modelocked oscillators with few-kHz optical linewidths of their femtosecond frequency comb are to be deployed [9], enabling a strong reduction of the anti-correlated amplitude noise in the ultrabroadband spectra of the few-femtosecond probe.
The theoretical studies of quantum aspects of electro-optic sampling carried out during the last years strongly support the claim that a time-domain quantum technology based on this method may eventually be established. For example, a subcycle description of squeezing was based on a time-flow approach [10]. The relevance of quantum contributions to the classical limit of the optical nonlinearity was studied in detail [11] and the role of back-action in the electro-optic detection process was clarified [12]. As soon as all obstacles are overcome, fascinating prospects emerge for experiments studying quantum electrodynamics in accelerated frames [13] and analogues of cosmological phenomena in curved spacetime [14].
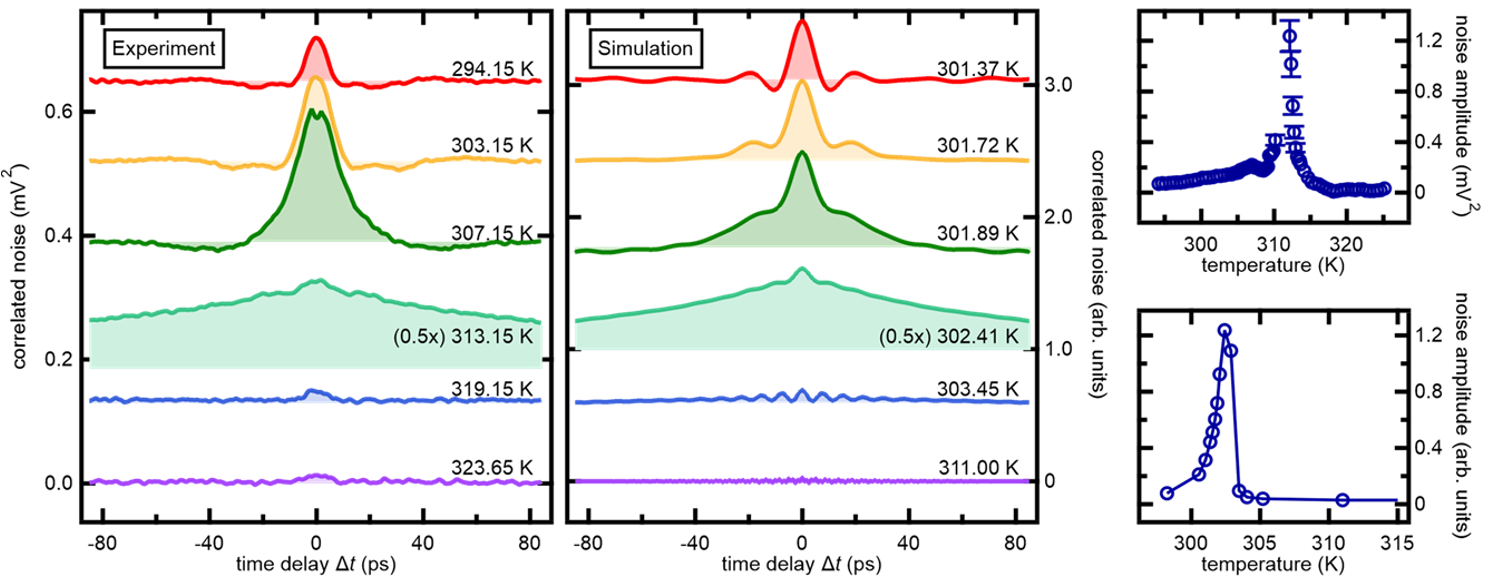
Figure 1: Femtosecond noise correlations during a spin-reorientation transition in antiferromagnetic Sm0.7Er0.3FeO3. Measurement (right) and atomistic simulation (center) of correlations in Faraday rotation amplitude as a function of time delay and at different temperatures. Right: Amplitude of magnetic fluctuations versus temperature over the phase transition in experiment (top) and theory (bottom).
Finally, another area of exciting applications for statistical readout of ultrafast experiments emerges in condensed-matter physics: harnessing an extension of the methodology from Ref. 4 and the Faraday effect, we managed to detect the correlations of spin fluctuations close to the reorientation phase transition in an orthoferrite by a time-domain approach with femtosecond resolution [15]. Fourier transform of those data not only yields temperature-dependent frequencies of magnon modes known from pump-probe and other spectroscopies but also phenomena like discrete jumps between degenerate energetic minima of the spin system that are inaccessible to conventional approaches (see Fig. 1).
References
[1] C. Riek, D. V. Seletskiy, A. S. Moskalenko, J. F. Schmidt, P. Krauspe, S. Eckart, S. Eggert, G. Burkard, and A. Leitenstorfer, Science 350, 420 (2015)
[2] A. S. Moskalenko, C. Riek, D. V. Seletskiy, G. Burkard, and A. Leitenstorfer, Phys. Rev. Lett. 115, 263601 (2015)
[3] C. Riek, P. Sulzer, M. Seeger, A. S. Moskalenko, G. Burkard, D. V. Seletskiy, and A. Leitenstorfer, Nature 541, 376 (2017)
[4] I.-C. Benea-Chelmus, F. F. Settembrini, G. Scalari, and J. Faist, Nature 568, 202 (2019)
[5] C. Beckh, P. Sulzer, N. Fritzsche, C. Riek, and A. Leitenstorfer, Journal of Infrared, Millimeter, and Terahertz Waves 42, 701 (2021)
[6] P. Sulzer, K. Oguchi, J. Huster, M. Kizmann, T. L. M. Guedes, A. Liehl, C. Beckh, A. S. Moskalenko, G. Burkard, D. V. Seletskiy, and A. Leitenstorfer, Phys. Rev. A 101, 033821 (2020)
[7] P. Sulzer, C. Beckh, A. Liehl, J. Huster, K. R. Keller, M. Cimander, P. Henzler, C. Traum, C. Riek, D. V. Seletskiy, A. Leitenstorfer, Opt. Lett. 45, 4714 (2020)
[8] H. Kempf, A. Muraviev, F. Breuning, P. G. Schunemann, R. Tenne, A. Leitenstorfer, and K. Vodopyanov, APL Photonics 9, 036111 (2024)
[9] S. R. Hutter, A. Seer, T. König, R. Herda, D. Hertzsch, H. Kempf, R. Wilk, and A. Leitenstorfer, Laser Photonics Rev. 17, 2200907 (2023)
[10] M. Kizmann, T. L. M. Guedes, D. V. Seletskiy, A. S. Moskalenko, A. Leitenstorfer, and G. Burkard, Nature Physics 15, 960 (2019)
[11] M. Kizmann, A. S. Moskalenko, A. Leitenstorfer, G. Burkard, and S. Mukamel, Laser Photonics Rev. 16, 2100423 (2022)
[12] T. L. M. Guedes, I. Vakulchyk, D. V. Seletskiy, A. Leitenstorfer, A. S. Moskalenko, and G. Burkard, Phys. Rev. Res. 5, 013151 (2023)
[13] T. L. M. Guedes, M. Kizmann, D. V. Seletskiy, A. Leitenstorfer, G. Burkard, and A. S. Moskalenko, Phys. Rev. Lett. 122, 053604 (2019)
[14] S. Onoe, T. L. M. Guedes, A. S. Moskalenko, A. Leitenstorfer, G. Burkard, and T. C. Ralph, Phys. Rev. D 105, 056023 (2022)
[15] M. A. Weiss, A. Herbst, J. Schlegel, T. Dannegger, M. Evers, A. Donges, M. Nakajima, A. Leitenstorfer, S. T. B. Goennenwein, U. Nowak, and T. Kurihara, Nature Communications 14, 7651 (2023)
