| PREVIOUS PRESENTATION | BACK TO PROGRAM OVERVIEW | NEXT PRESENTATION |
Ionization-Induced THz Emission
S. Skupin1, H. Alirezaee2, I. Babushkin3, and L. Bergé4
1Institut Lumière Matière, UMR 5306 – CNRS, Université de Lyon 1, 69622 Villeurbanne, France
2Center for Research on Laser and Plasma, Shahid Chamran University for Ahvaz, Iran
3Institute of Quantum Optics, Leibniz University Hannover, Welfengarten 1, 30167 Hannover, Germany
4Centre Lasers Intenses et Applications, Université de Bordeaux–CNRS–CEA, 33405 Talence Cedex, France
The generation of strong broadband THz fields by two-color laser-induced plasmas has attracted significant attention because of the high amplitude and broad spectral width of the radiation emitted [1]. The mechanism is based on photocurrents produced by ionization in an asymmetric driving field consisting of the fundamental pulse and its second harmonic [2]. Thus, THz emission is inextricably related to ionization, and its properties have recently been suggested to reveal valuable information about the ionization process itself [3]. Considerable effort has been devoted to optimizing and controlling various characteristics of the THz radiation produced. In particular, the efficiency of THz generation was shown to be influenced by the relative phases between harmonics [2]. Other important factors affecting the produced THz radiation are pump wavelengths [4], polarization of the pulses [5], their durations [6] and, more generally, their wave shapes [7].
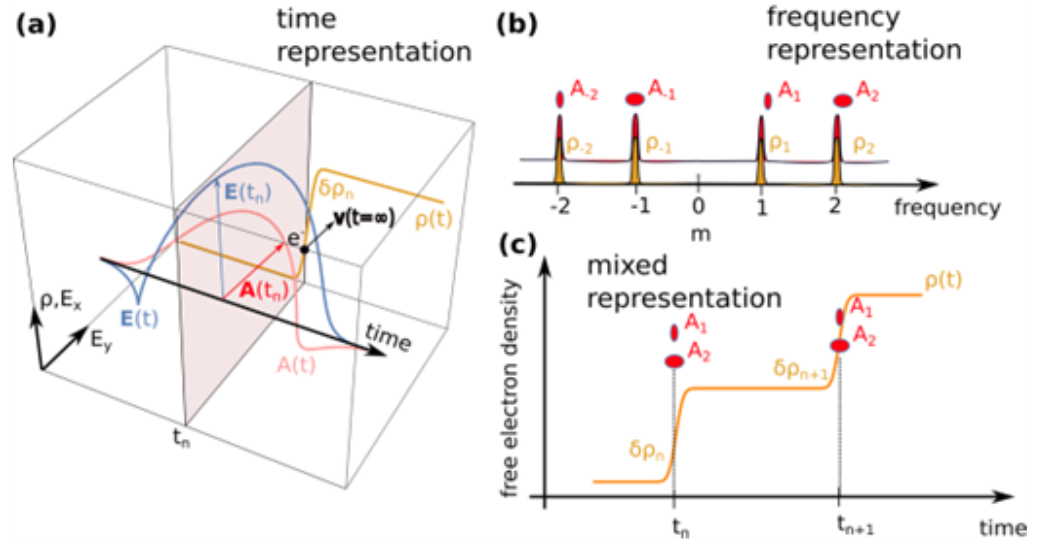
Figure 1: Predicting the THz wave shape: (a) Time representation: Uses information on the vector potential A(tn) of the pump in the vicinity of the ionization event tn and the corresponding ionization step δρn. (b) Frequency representation: Uses the Fourier components Am and ρm of the pump and electron density. (c) Mixed representation: Uses the Fourier components Am of the pump, the ionization steps δρ\sub>n in the time domain, and its phase information exp(imtnω0).
We will review the ionization induced THz generation and explain its main characteristics in the local current framework — the locally generated THz waveforms in a small space volume. Three equivalent representations are developed, which allow for a convenient interpretation of difference characteristics, cf. Figure 1. We study the variety of possible THz waveforms, which can appear in two- and multicolor schemes with arbitrary polarization of the pump pulses, with focus on the polarization state of such THz radiation. Starting from general principles, we show how the elliptically polarized THz radiation arises, which degrees of polarization of the THz pulse are possible, and to what extent these can be controlled by the pump configuration. We illustrate our findings by systematically studying the dependence of the THz waveshape on the pump configuration for a two-color scheme with controlled polarization and phase difference between the pump frequency components.
References
[1] M. Kress et al., Opt. Lett. 29, 1120 (2004). I. Babushkin et al., PRL 105, 053903 (2010). A. D. Koulouklidis et al., Nat. Comm. 11, 292 (2020).
[2] K. Y. Kim et al., Opt. Express 15, 4577 (2007).K. Y. Kim et al., Nat. Phot. 2, 605 (2008). I. Babushkin et al., New J. Phys 13, 123029 (2011).
[3] F. Brunel et al., J. Opt. Soc. Am. B 7, 521 (1990). I. Babushkin et al., Nat. Phys. 18, 417 (2022).
[4] M. Clerici et al., PRL 110, 253901 (2013). A. Nguyen et al., Opt. Lett. 44, 1488 (2019). V. Y. Fedorov et al., Light Sci. Appl. 9, 186 (2020).
[5] C. Meng et al., Appl. Phys. Lett. 109, 131105 (2016). O Kosareva et al., Opt. Lett. 43, 90–93 (2018). C. Tailliez et al., New J. Phys. 22, 103038 (2020).
[6] T. Bartel et al., Opt. Lett. 30, 2805 (2005). T. J. Wang et al., Appl. Phys. Lett. 95, 131108 (2009). C. Lu et al., Phys. Rev. A 92, 063850 (2015).
[7] P. González de Alaiza Martı́nez et al., PRL 114, 183901 (2015). A. Nguyen et al., New J. Phys. 20, 033026 (2018)
